Matemáticas GUIA # 7

SEPTIEMBRE 29-2020

INSTITUCION EDUCATIVA OCTAVIO HARRY-JACQUELINE KENNEDY

DANE 105001003271 - NIT 811.018.854-4 - COD ICFES 050963 // 725473

Código: FA 21

Fecha: 20/04/2020

Guía de aprendizaje por núcleos temáticos

---

Docente:

Luz Adriana Quintero Ruiz

Período:

3°

Año:

2020

---

Grado:

5°

Áreas por Núcleos Temáticos:

Matemáticas- Geometría- Estadística

---

Objetivos de grado por núcleo temático:

1. Apropiar la noción de razón entre dos cantidades

2 - Hallar la razón entre dos cantidades.

3 - Determinar una proporción a partir de dos razones dadas.

4 - Establecer diferencias entre razón y proporción.

5- Dibujar segmentos y ángulos congruentes entre sí.

---

Competencias:

La formulación, el tratamiento y la resolución de problemas.

La modelación

El razonamiento

La formulación, comparación y ejercitación de procedimientos.

---

Indicadores de desempeño:

1. Interpreta situaciones referidas a proporciones directas e inversas. (RP)

Identifica y describe relaciones inversamente y directamente proporcionales

2. Identifica dos polígonos semejantes si todos sus ángulos y lados correspondientes son congruentes entre sí.

3. Interpreta y soluciona situaciones problema en diferentes contextos.

GUIA # 7

TEMATICAS

*Razón y proporción

*magnitudes directamente proporcionales

*magnitudes inversamente proporcionales

*porcentajes

*relación entre los porcentajes, las fracciones y números decimales

*figuras semejantes y congruentes

*lectura e interpretación de grafica de barras

ORIENTACIONES GENERALES:

 Las actividades se pueden desarrollar en el cuaderno o en el block (algunos puntos se desarrollan en la misma guía, según la instrucción).

 Cuando envíes las evidencias de estudio en casa, ya sean por Whats App o por correo electrónico, por favor indicar: Nombre del estudiante, materia y tema.

 Todas las fichas o imágenes que encuentres a blanco y negro se deben de colorear.

 Enviar evidencias sólo de las actividades, no es necesario tomarle fotos a la teoría de las guías.

 Al compartir las evidencias, tratar de que las fotos queden nítidas y completas, ya que han sucedido casos, que al descargarlas, se ven borrosas o mochas.

 Enviar las evidencias de un trabajo, una vez terminados todos los puntos de dicha actividad, no enviar puntos separados en diferentes días. Todo completo y en orden, durante la fecha establecida.

 Es importante recordar, que para atención de dudas e inquietudes, puede escribirnos al chat del Facebook o al whats app de lunes a viernes en el horario de 8am a 2pm, que con mucho gusto los atenderemos. Si en ocasiones no es posible responder de inmediato, se hará la devolución del mensaje de acuerdo a la disponibilidad de tiempo durante la jornada.

 Enviar las evidencias a los contactos de las docentes que dicten las respectivas áreas:

• Luisa Fernanda Ochoa Henao:

WhatsApp: 3054879060 – Correo electrónico: profelu2020@gmail.com

• Luz Adriana Quintero Ruìz:

WhatsApp: 3196708908 – Correo electrónico: linamonsalvequinto@gmail.com

RAZON Y PROPORCION

RAZON: Una razón es la comparación entre

dos cantidades expresada en forma de cociente

PROPORCION

: Una proporción es la igualdad entre dos razones, los términos primero y cuarto son extremos y el segundo y el tercero son los medios. En toda proporción el producto de los extremos es igual al producto de medios.

EJEMPLO

MAGNITUDES DIRECTAMENTE PROPORCIONALES

Para que dos magnitudes mantengan una relación de proporcionalidad directa tienen que estar relacionadas de tal forma que si duplicamos una, la otra se tiene que duplicar, si la triplicamos la otra también y si la reducimos a la mitad la otra también se tiene que reducir. Se puede entender que si aumentamos la cantidad de una, la otra tiene que aumentar también proporcionalmente.

EJEMPLO

¿Qué relación podemos ver entre el número de plátanos y el número de cajas que necesitamos para guardarlos

Es importante saber que el cociente (razón o proporción) entre dos magnitudes directamente proporcionales es siempre constante. En nuestro ejemplo tenemos que la razón es 3.

Las relaciones de proporcionalidad aparecen con mucha frecuencia en nuestra vida cotidiana.

¿Alguna vez habéis comprado caramelos? ¿Cómo calculabais la cantidad de dinero que teníais que pagar por los caramelos?

MAGNITUDES INVERSAMENTE PROPORCIONALES

Tenemos 2 magnitudes (A y B) y vemos la relación que existe entre las dos:

Si A aumenta entonces B disminuye. Entonces la proporción entre las dos magnitudes es inversa.

Por ejemplo, en la siguiente tabla se muestran las magnitudes A y B:

Es una proporcionalidad inversa porque a medida que aumenta A disminuye B.

¿Cómo se aplica la regla de tres inversas?

Esta resolución se aplica a los problemas de proporcionalidad en los cuales se conocen tres de los cuatro datos que componen las proporciones y se requiere calcular el cuarto.

Primero hacemos la relación entre A y B. Después escribimos la relación que nos preguntan.

C es un valor de la magnitud A, y X es el valor de la magnitud B que tenemos que hallar.

¿Cómo resolvemos un problema con la regla de tres inversas?

EJEMPLO 1.

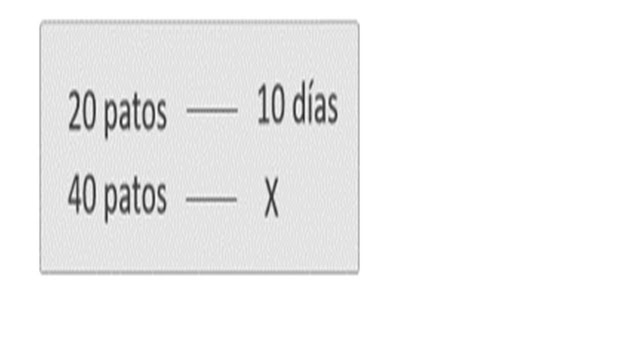
En una granja, 20 patos tardan 10 días en comer el alimento que hay guardado. ¿Cuánto tiempo tardarán 40 patos en terminar el alimento?

Primero tenemos que comprobar si la proporcionalidad es directa o inversa:

20 patos tardan 10 días. 40 patos, ¿tardarán más o menos días?

Al haber más patos, se acabará antes el alimento que hay guardado, por lo que tardarán menos días

Si la cantidad de patos aumenta, el número de días disminuye. Entonces es proporcionalidad inversa.

Ahora aplicamos la regla de 3 inversa:

40 patos tardarán 5 días en comer todo el alimento.

EJEMPLO 2.

3 pintores tardan 12 días en pintar una casa. ¿Cuánto tardarán 9 pintores en hacer el mismo trabajo?

Primero vamos a ver qué tipo de proporcionalidad es.

3 pintores tardan 12 días. 9 pintores, ¿tardarán más o menos días?

Al haber más pintores, tardarán menos tiempo en terminar el trabajo. Entonces, es proporcionalidad inversa.

Ya podemos aplicar la regla de tres inversas:

9 pintores tardarán 4 días en pintar la casa

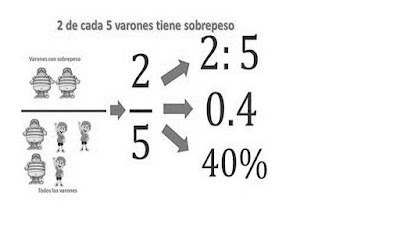
PORCENTAJES

un porcentaje es una medida matemática que representa una parte de un total.

Siempre que hablemos de calcular porcentajes nos estaremos refiriendo a una parte de algo.

El método más importante y principal que debes conocer para poder calcular un porcentaje es el siguiente

El porcentaje de algo siempre se calcula usando la multiplicación y luego la división. Siempre éste será el orden y no a la inversa. Debes tener en cuenta esto.

Multiplica el número total por el porcentaje y Divide el resultado obtenido por 100.

Veamos un ejemplo: supongamos que tenemos que calcular el 12% de 48.

Primero tenemos que determinar cuál es el total. En este ejemplo el total es 48 y necesito calcular el 12% de 48

Entonces, el 12 % de 48 es 5,76

DESARROLLO DE ACTIVIDADES

Inversa _____ Directa ______ Justifica tu respuesta _______________

Inversa_____ Directa____ Justifica tu respuesta_______________________

2. RESUELVE LOS SIGUIENTES PROBLEMAS Y DIGA SI ES UNA PROPORCIONALIDAD INVERSA O DIRECTA

A-) En 50 litros de agua de mar hay 1.300 g. de sal. ¿Cuántos litros hacen falta para 5.200 g. de sal?

B.-) Un coche gasta 5 litros de gasolina cada 100 kms. ¿Cuántos kms. recorrerá con 28 litros?

C. )5 Obreros hacen una pared en 15 días. ¿Cuánto tardarán 3 obreros en hacer la misma pared?

D.) Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos dijeron que 5 centímetros del mapa representaban 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?

E.) Ayer 2 camiones transportaron una mercancía desde el puerto hasta el almacén. Hoy 3 camiones, iguales a los de ayer, tendrán que hacer 6 viajes para transportar la misma cantidad de mercancía del almacén al centro comercial. ¿Cuántos viajes tuvieron que hacer ayer los camiones?

3.) Determine el número decimal correspondiente a cada porcentaje:

a) 20 % b) 75% c) 140% d) 2% e) 6,2% f) 3 %

4.) Exprese cada porcentaje en forma de fracción irreductible:

a) 35 % b) 40 % c) 140 % d) 2% e) 6,2% f) 135 %

5.) Determine el porcentaje que corresponde cada número decimal

a) 0,67 b) 0,138 c) 1,59 d) 0,07 e) 2,325

6.) Calcule:

a) el 30% de 90 b) el 45% de 60 c) el 130% de 75 d) el 150% de 4600 e) el 3% de 14,7

f) el 2,5% de 10 g) el 0,08% de 12000

7.) a) ¿Qué tanto por ciento representa 45 de 180?

b) ¿Qué tanto por ciento representa 345 de 1500?

c) ¿Qué tanto por ciento representa 26,6 de 38?

d) ¿Qué tanto por ciento representa 22 de 25?

e) ¿Qué tanto por ciento representa 925 de 1250?

8.) a) Determine una cantidad sabiendo que el 12% de ella es 87.

b) Si el 62% de una cantidad es 93, ¿cuál es la cantidad?

c) Determine una cantidad sabiendo que el 12% de ella es 87.

9.) Resuelve

a) adquirir un auto cuyo precio es de $38.000.000, nos hacen un descuento del 4.5%.

¿Cuánto debo pagar por el vehículo?

b) El precio de una caja de chocolate, sin IVA, es de $ 1750. Sabiendo que el IVA es

el 4%, ¿cuál será su precio con IVA?

10) Una empresa dispone de dos talleres, A y B, en los cuales se fabrican zapatillas deportivas.

Se considera una producción total de 5000 pares de zapatillas.

• El 70 % de los pares de zapatillas se fabrican en el taller A y el resto en el taller B.

• El 3 % de los pares de zapatillas que se fabricaron en el taller A, están defectuosas.

• El 2 % de los pares de zapatillas que se fabricaron en el taller B, están defectuosas.

GEOMETRIA

FIGURAS SEMEJANTES Y CONGRUENTES

FIGURAS SEMEJANTES: En matemáticas se dice que dos figuras geométricas son semejantes si tienen la misma forma sin importar los tamaños entre ellos.

EJEMPLO

Para saber si dos figuras son semejantes se deben de identificar algunas propiedades:

1. Misma forma

2. Mismos ángulos

3. Medidas proporcionales

Ejemplo

Figuras congruentes: son aquellas figuras que son exactamente iguales, tienen la misma forma, el mismo tamaño, las mismas medidas al igual que sus angulos.

Ejemplo